Penmachine

I've never properly understood what the focal length of a modern camera lens really is. I'd bet that many amateur and even professional photographers don't either, even though we use the term all the time. This blog post is my attempt to get it straight in my own mind, at least in a simple enough way to help the rest of this series make sense.

While I wrote in my introduction that these articles would be short, this first one is longer than average because focal length is so important to understanding everything else about lenses and cameras.

Focal lengths for film and "full frame" digital cameras

Things were a little simpler in the pre-digital age, when most people were using 35 mm film, but those numbers are still unintuitive for most people. For those film cameras, and for the very few high-end modern digital single-lens reflex (SLR) cameras with so-called "full-frame" sensors, picture-taking enthusiasts know a few things:

• If you want to get a decent-sized photograph of something far away, you need a telephoto lens, one with a long focal length, like 135 mm or 200 mm or 300 mm, or even more.
• If you instead want a picture of a group of people in a small room, or the whole of a panoramic landscape, you need a wide-angle lens, with a short focal length, perhaps 35 mm or 28 mm or 21 mm, or even less.
• For photos that look similar to what you might see with your own eyes (i.e. near and distant objects look in proper proportion), you need a normal lens, with a medium focal length around 43 mm or 50 mm or 55 mm.

But why is that? What is the focal length of a lens, and why does it have anything to do with how close or far from your subject you need to be in order to fit it in your picture?

What is focal length?

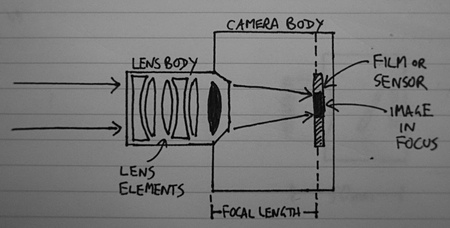
For a simple, single-element lens, the focal length is the distance between the middle of the lens and the focal point, where parallel light rays get concentrated to a point. As a kid you might have tried burning paper (or, less kindly, insects) at the focal point of a magnifying glass, for example:

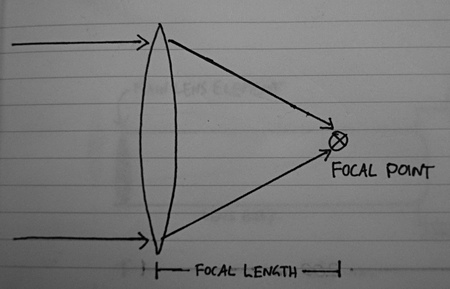
PLEASE NOTE: None of my quickie diagrams here are drawn to accurate scale.

Things aren't quite so simple for camera lenses, because they're made not of one piece of glass, but of several glass elements stacked next to each other to allow for variable focusing, correct for distortions and aberrations, and so on. And usually they're not trying to focus sunlight to a burning point either; rather, they project an in-focus circular image onto the focal plane of the camera, which is where the digital sensor (or, formerly, strip of film) sits:

Photo above: With the lens removed, shutter open, and mirror flipped up, you can see right through the body of my Nikon F4 camera to the focal plane at the back, where the film would be.

All those extra pieces of glass result in all sorts of focal length ratios, indexes of refraction, and ultimately equations, which when you run the numbers spit out the focal length of the lens. But it's fundamentally the same basic idea as the focal length of a simple lens, and the way I like to think of it is this:

• For a lens with a focal length of 50 mm, if you turn the focus ring to infinity (i.e. as far as the lens can focus), then the focal length is the distance between the main glass element of the lens (wherever that may be inside the lens itself) and the film or sensor surface at the back of the camera. And in this case that's 50 mm (5 cm, or about two inches).

Similarly, in a 200 mm lens, the distance is 20 cm, or about 7.9 inches. In a 21 mm lens, that lens-to-sensor distance will be 21 mm, which is 2.1 cm (less than an inch), and so on^*:

Again, please keep in mind that real camera lenses aren't built quite like this. Rather, I imagine them being built this way to help understand how the camera works.

By the way, it turns out that when you focus closer than infinity, such as on a person a couple of metres away from the camera, the main lens element needs to move away from the film plane very slightly (usually only a millimetre or two for a normal lens) to keep the image sharp. So that's why you see lens elements move in and out when you turn the focus ring:

Photos above: My AF Nikkor f/1.8D lens at infinity focus (left) and closest focus (right). Notice how the lens element moves forward, away from the camera body (which would be on the right when attached) as you focus closer.

There are also lots of ways that lens designers use multiple glass elements in modern lenses so that the actual lens-to-sensor distance doesn't match the focal length (hence those equations I talked about a few paragraphs back).

But let's pretend they don't do that, okay? Because we still don't know why shorter focal lengths are wide angle and longer ones are telephoto, do we? Let's figure that out.

Focal length and angle of view

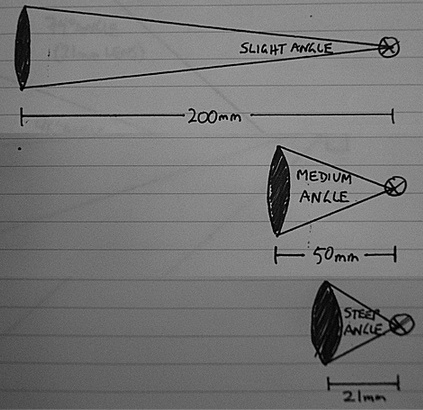
Imagine three lenses with different focal lengths: 200 mm, 50 mm, and 21 mm. Each has to bend incoming light a different amount:

• The 200 mm lens bends the light at a very slight angle, to get it to focus 200 mm (20 cm) behind the lens. (This distance from the focal plane also explains, in part, why telephoto lenses stick out farther from the camera body than normal or wide-angle lenses.)
• The 50 mm lens bends it more, at a steeper, medium angle, because the focal plane is only one-quarter as far away.
• The 21 mm lens has to bend the light a lot, at a steep angle, to get it to focus a mere 21 mm behind the lens, almost ten times closer than the 200 mm lens.

Okay, we know (sort of) what's going on with the light behind the lens, inside the camera. What about the light the lens collected in front of the lens, before it got all bent? Let's extend my simplified mental picture of each lens to the left a bit, out to the subject of the photograph:

Follow the lines of the bent light backwards (to the left in my diagram), out to the subject for each lens:

• Because the 21 mm lens is bending the light at such a steep angle, it's essentially sucking in light from a much wider area in front of the camera. For a regular film camera, that angle of view is about 74° across.
• The 50 mm lens, with its shallower angle, sucks in light from a narrower field in front of the camera: 46°, in this case.
• The 200 mm lens projects its image with a very narrow angle, and so sucks in light from an area only 12° across in front of the camera.

The angle of the cone of light that each lens is sucking in is known as its angle of view or field of view. Imagine pointing each of those lenses at a city skyline:

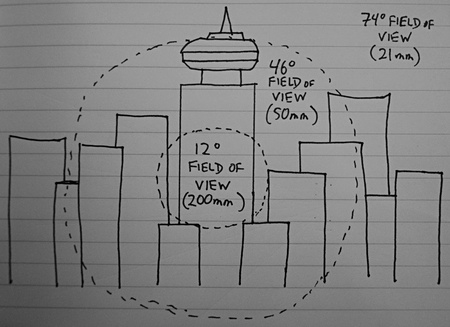
Remember, I didn't draw these diagrams to an accurate scale. Please don't measure the circles and tell me they're the wrong size (or that they're not circular, for that matter).

The 21 mm lens will see the whole skyline: a wide-angle view. The 50 mm lens will see a few buildings, which is a normal view for your eyes. And the 200 mm lens might see a few floors of a single building: a telephoto view.

Ta da! Now you know why each type of lens has a certain focal length.

Further questions

Okay, great, so a lens's angle of view depends on its focal length. Spiffy. You might be wondering a couple of other things, such as:

• Why aren't the price and complexity of a lens directly related to the focal length? Normal lenses (with medium focal lengths) are both less expensive and less bulky than either telephoto ("long") or wide angle ("short") lenses. That seems weird.
• Why do zoom lenses, which let you rotate or slide the barrel of the lens to change the focal length without changing lenses, have compromises in size, weight, price, and performance compared to fixed–focal-length ("prime") lenses?

The answers to those questions require knowing more stuff, which is why next time we'll talk about apertures and f-numbers.

^*SEMI-RELEVANT SIDE NOTE: From this simplified perspective, you can understand why some old fisheye super-wide lenses from the '60s, which had focal lengths of 8 mm or less, forced you to flip up the mirror inside the camera to use them. The rear lens element had to sit 8 mm (less than a third of an inch) from the film plane, so those lenses had to stick waaay back into the camera body—so far that they would hit the mirror and crack it if you didn't move it out of the way.

Newer fisheye lenses use multi-element design tricks to keep the rear lens element in front of the mirror and avoid that problem. But no, I don't know the math of how that works, so I'll just think of it as lens-design magic for now.

Read more

Some useful resources:

• Wikipedia: The Science of Photography
• The Field of View Thing
• Tips and Trick: Focal Length
• Understanding Camera Lenses

« Previous: introduction

Next: f-stop teaser »

Labels: barcamp, cameraworks, geekery, photography