Penmachine

The pupil of your eye is an amazing adaptation. In bright light, your brain tells tiny muscles at the front of your eyeball to close your pupils down to miniscule circles, and when that happens you're not blinded. If you're like me and need strong glasses, take your glasses off and you'll also notice that in bright light things are a little less blurry than otherwise.

In dim light, your brain tells the muscles to open your pupils up wide, and you can see better in the dark (although it takes the rest of your optical system a few minutes to adjust its sensitivity to compensate, and human night vision is pretty lousy compared to that of many other animals). When you get your eyes checked, the ophthalmologist's annoying eyedrops trick your eye muscles into opening the pupils all the way, so that the coloured part of your irises almost vanish around the edges. You might notice then that even with glasses on, you can't focus properly, or read a book or computer screen.

Building lenses to work like the human eye

Camera lens designers take many cues from eyes, and one of the main ones is having an iris (the lens diaphragm) inside the lens that can open or close to let more or less light through. Instead of using muscles and tissues, camera lens diaphragms have a set of thin, overlapping pieces of metal known as aperture blades, and instead of the pupil, the opening in the middle is the aperture:

There are seven metal diaphragm blades in this lens, which open and close the central aperture. Other lenses may have more or (rarely) fewer blades, and in some designs the edges of the blades might be curved so the aperture is more like a circle than a straight-edged polygon.

As in the human eye, the aperture lets the photographer (or the camera's exposure computer) increase or reduce the amount of the light that gets through to the film or sensor at the back of the camera body. But why would you want to do that? Why not let in as much light as possible all the time?

Depth of field, speed, and sensitivity

There are three main reasons to vary the lens aperture:

• To control the depth of field (also known as the depth of focus) of the image.
• To permit shooting at either a faster or slower shutter speed.
• To use greater or lesser sensitivity (often called "ISO") for your film or digital sensor.

Depth of field refers to how much of a photograph is in focus, like this:

On the bottom left, an image with little (shallow) depth of field, using a wide aperture (see the lens on top left). All you can see clearly is the laptop screen. On the bottom right, the same shot with greater (deep) depth of field, using a small aperture (see the lens on top right). You can now see my foot, the bed, and the dressers in the background.

In both photographs, the laptop closest to the camera is in focus. With little depth of field (on the left), everything in the background is blurry. With more depth of field (on the right), not only can you see the laptop in focus, you can also see my sock, a book on the bed, and the bedroom dressers in the background, also largely in focus. If you closely, you can even see that the reflections in the screen of the laptop are blurry on the left, but sharper on the right.

The physics of light rays, and the way they refract and diffract inside lenses and apertures, means that when the aperture is really small, the resulting image has greater depth of field—just like your eyes on a sunny day. (A pinhole camera, which has an extremely tiny aperture, offers such great depth of field that it doesn't need a lens at all.)

And when the aperture is really large, the depth of field is shallower, just like when you get eyedrops at the ophthalmologist's office—and can't even read a newspaper because it's so blurry. So depending on how much of your image you want in focus, you're going to set the aperture differently. For a portrait with a nice soft background, you'll choose a large aperture. For an image where both nearby and distant objects need to be in focus, you'll choose a small aperture:

Left, large aperture, shallow focus (even my younger daughter's hair is a little out of focus, but her eyes are sharp). Right, small aperture, deep focus (my older daughter's dress is in focus, but so is everything else, including the distant clouds).

Of course there's a tradeoff. The smaller the aperture of the lens, the less light gets through, and so either:

• You'll have to expose the film or sensor longer to get the same amount of light on it, or...
• You'll have to increase the sensor sensitivity (or use faster film) to collect the light more efficiently.

But that can work to your advantage too, even ignoring depth of field:

• If you're photographing fast-moving things (sports, cars, kids, aircraft, birds in flight) or otherwise want to freeze the action, use a large aperture so you can use a fast shutter speed, since you're letting in more light.
• If you want to minimize film grain or sensor noise, use a large aperture with lower sensor sensitivity or slower, more fine-grained film.
• If you want a long exposure (to make the water in a waterfall look soft, or to blur motion so it looks like motion, or to get streaks of light from cars driving at night), use a small aperture to let in less light so you can use a slower shutter speed.
• If it's really, really bright out (a sunny day on a snowy ski hill or sandy beach), use a small aperture to avoid overloading the sensor or film.

Small and large apertures now make sense, because they give you a lot of creative control over your images, and let you adjust your picture-taking to your subject, the light, and your photographic conditions. But why are the numbers that photographers use for them, like f/1.8 and f/5.6 and f/22, so strange? What do those numbers mean, and why do the larger numbers represent smaller apertures?

What is an f-stop?

The specific setting of a lens aperture at any time is called its f-stop. (We'll see why below.) On almost all modern cameras, including big single-lens reflex (SLR) models, you adjust the f-stop with buttons or control dials, but for most of the 20th century, photographers did so by adjusting the aperture ring on the body of the lens. Many lenses still include an aperture ring for compatibility with older cameras:

The aperture ring on my 50 mm lens here is set to f/8 (the "8" below the white dot), about midway through its range.

The f-stops available range from small numbers (like 1.8 or 2.8 or 3.5) to large (like 16 or 22 or 32). Counterintuitively, the small numbers represent large apertures (on this lens, f/1.8 is wide open and lets in the most light, for instance), while the large numbers are small apertures (f/22 is the smallest aperture, letting in the least light).

To show why, we'll do some really simple math. First, here's a diagram of where the aperture might be in a typical camera lens with multiple glass elements in it:

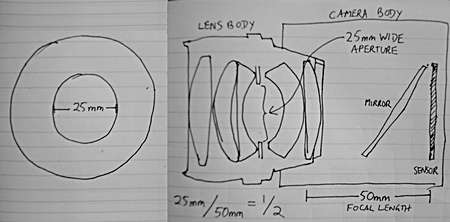
A lens looked at two ways: On the left, looking straight into the front, with the aperture open to a width of 25 mm. On the right, a cross-section of the side (with its multiple glass lens elements), with the lens attached to the camera, again with the aperture open to 25 mm, and showing this lens's focal length of 50 mm.

The f-stop setting of a lens is the ratio between the diameter of the aperture and the focal length of the lens:

Another way to write that is aperture diameter : focal length. In this example, we have 25 mm aperture : 50 mm focal length, which is 1 : 2. Another way to say it is that the aperture is (in this case) half the focal length, or f/2. A photographer would pronounce that "eff-two." Since the widest aperture of a lens is important to know, lenses are usually specified that way, so you could buy a lens labelled as a 50 mm f/2 or 50 mm 1:2 lens.

Yet another way to think of it is that it would take two apertures of that width to equal the focal length of the lens.

Let's look at a bunch of other f-stops for my lens:

My 50 mm lens set to apertures of (from left to right) f/1.8, f/4, f/8, and f/16.

At f/1.8, the aperture is about 27.8 mm across, and it would take 1.8 of them to equal the focal length of the lens. At f/4, you'd need four of the 12¹/₂ mm apertures to equal the focal length. At f/8, you'd need eight 6¹/₄ mm apertures to equal the focal length. At f/16, you'd need 16, since the aperture is only 3¹/₈ mm across.

But why isn't the lens aperture ring simply marked with those diameters? Why doesn't it read 27.78, 17.86, 12.5, 8.93, 6.25, 4.55, 3.125, 2.27 instead of 1.8, 2.8, 4, 8, 11, 16, 22? There's a good reason, and it's the clever part.

F-numbers work for any lens, however you measure it

The cool thing is when you start to use different lenses, or different cameras. For a given amount of light entering a lens, a particular f-stop always lets the same amount of light through to the sensor or film—and it doesn't matter what focal length the lens is or what kind of camera you're using!

Here's why that's important. We already know that when a 50 mm lens is set at f/2, the aperture is open 25 mm (see my diagram above). But what about a 200 mm telephoto lens (four times the focal length)? To be open to f/2, that lens's aperture would have to be open half that lens's focal length, an opening 100 mm in diameter (four times as wide). And a 24 mm wide-angle lens? At f/2, its aperture is open only 12 mm, or half its focal length.

So if the apertures of every lens were labeled with their actual widths, every lens would be different. The aperture ring on a 200 mm lens might read:

100.00, 71.42, 50.00, 35.71, 25.00, 18.18...

But a 24 mm lens would be:

12.00, 8.57, 6.00, 4.29, 3.00, 2.18...

Even worse, to take a photo of the same scene under the same lighting conditions, you'd set the 200 mm lens to aperture 35.71, but set the 24 mm lens to aperture 4.29—both to get exactly the same amount of light to your film or sensor. If you think f-stops are confusing now, imagine how confusing that would get.

Instead, I know that a 200 mm lens set to f/5.6 lets through the same amount of light as a 24 mm lens set to f/5.6, and the same as a 50 mm lens set to f/5.6. I even know that if I could get myself an 8 mm fisheye lens, or a 600 mm super-telephoto, those lenses would also let through the same amount of light at f/5.6. For a given brightness of a scene, any lens set to the same f-stop can use the same shutter speed and sensitivity to get a proper exposure.

That's why f-stops are a good way to measure aperture, and why we put up with having big numbers mean small openings. But there's one last thing.

Why those particular aperture and shutter stops?

Okay, so if we're going to use f-numbers, why aren't they a more sensible sequence, like 1, 2, 3, 4, 5... or at least 2, 4, 8, 16, 32...? Why those weird ones in the middle, like 2.8 and 5.6 and 11?

That's because each stop on the aperture ring doubles the amount of light hitting the focal plane, if you're opening it wider, or cuts it in half, if you're closing it down. (Most of the time, anyway—sometimes the widest aperture doesn't exactly double the light from the next-widest, just because the lens isn't designed to open any wider. So my lens opens to f/1.8 instead of f/1.4.)

Imagine your lens is set to f/5.6 and the light meter says a proper exposure is 1/250th of a second. You can open the lens up one stop, to f/4, and twice as much light gets through. So you can make the shutter speed twice as fast, 1/500th of a second, and still get the right exposure.

This explains why the shutter settings are the way they are too, as shown on the shutter speed dials of older cameras. Click your lens aperture ring one stop wider (f/5.6 to f/4), and you can click the shutter speed ring one stop too, to the next faster speed (from 1/250th of a second to 1/500th).

Click the shutter speed four stops slower (say, from 1/1000th of a second to 1/60th of a second), and you need to close the aperture of the lens four stops narrower (from f/4 to f/16) to get the same exposure.

There's a little bit of convention and standardization in all those numbers. Each f-stop, letting in twice the light, represents an increase in diameter of a factor of the square root of 2 (written as ), which is about 1.4142. Multiply 1.4142 by itself and you get 2. Multiply that by 1.4142 again and you get 2.8284. Multiply that by 1.4142 and you get 4. Multiply that by 1.4142 and you get 5.6568. Round that series out and you get:

1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22...

Look familiar? It's all in the physics of light passing through roughly circular holes. Increase the diameter of a hole by 1.4 times or so, and you double the light getting through. Why is that? That takes a bit more math. Remember the formula for the area of a circle from math class? To remind you, it's πr², where r is the radius of the circle, i.e. half the diameter.

If you want to double the area of a circle (and thus double how much light it lets through), you need to multiply the value of r² by 2. To do that, you multiply r by the square root of 2 (), or about 1.4. And when the radius increases by 1.4 times, so does the diameter, which is the width of the little pupil that lets light through the aperture blades of the lens. And that's why each f-stop on your lens is 1.4 times the value of the previous one. One stop larger, double the light. One stop smaller, half the light.

The same for shutter speed numbers, but there it's even simpler, because you don't need any area-of-a-circle calculations. Each faster shutter stop lets in half the light, because the shutter is open half as long. Take a one second exposure. To get half the light, make it 1/2 second. Half that is 1/4, then 1/8th of a second, then 1/16 (conventionally abbreviated to 1/15), then 1/32 (or 1/30, which is close enough for photographic tolerances), 1/64 (or 1/60), 1/128 (close to 1/125th), and so on. So your shutter speed dial reads:

1, 2, 4, 8, 15, 30, 60, 125, 250, 500, 1000...

My guess is, if history were skewed and photography had been invented after digital computers, things would be different. We've all gotten used to powers of two (like 32, 64, 128, 256, 512, 1024, 2048, etc.), so we'd have those kinds of numbers on the shutter speed dial and on our digital camera LCD screens instead of the rounder numbers we see now.

Read more

Some useful resources:

• Wikipedia: The Science of Photography
• Wikipedia: F-number
• Understanding Camera Lenses
• Controlling Light

« Previous: f-stop teaser

Next: crop factor & digital lenses »

Labels: barcamp, cameraworks, geekery, photography